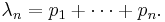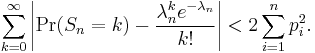Le Cam's theorem

In probability theory, Le Cam's theorem, named after Lucien le Cam (1924 – 2000), is as follows.

Suppose:

X₁, ..., X_n are independent random variables, each with a Bernoulli distribution (i.e., equal to either 0 or 1), not necessarily identically distributed.

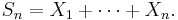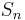$S_n = X_1 %2B \cdots %2B X_n.\,$ (i.e. $S_n$ follows a Poisson binomial distribution)

Then

$\sum_{k=0}^\infty \left| \Pr(S_n=k) - {\lambda_n^k e^{-\lambda_n} \over k!} \right| < 2 \sum_{i=1}^n p_i^2.$

In other words, the sum has approximately a Poisson distribution.

By setting p_i = 2λ_n²/n, we see that this generalizes the usual Poisson limit theorem.

References

Le Cam, L. (1960). "An Approximation Theorem for the Poisson Binomial Distribution". Pacific Journal of Mathematics 10 (4): 1181–1197. MR 0142174. Zbl 0118.33601. http://projecteuclid.org/euclid.pjm/1103038058. Retrieved 2009-05-13.
Le Cam, L. (1963). "On the Distribution of Sums of Independent Random Variables". Bernoulli, Bayes, Laplace: Proceedings of an International Research Seminar. New York: Springer-Verlag. pp. 179–202. MR 0199871.
Steele, J. M. (1994). "Le Cam's Inequality and Poisson Approximations". The American Mathematical Monthly 101 (1): 48–54. doi:10.2307/2325124. JSTOR 2325124. edit